Chapter 1: The Foundations of Computational Thought

The concept of computing has undergone significant evolution, especially with the introduction of the universal Turing machine. This theoretical construct was developed by mathematician and computer scientist Alan Turing in the 1930s, demonstrating that a machine capable of executing any algorithm on any input could exist. By 1945, physicist John von Neumann contributed a tangible blueprint for such a machine, which included:

• A processing unit for executing calculations
• A memory unit for storing data and instructions
• A mechanism for input and output operations

This architecture, known as the von Neumann model, forms the basis for nearly all contemporary computers and is classified as Turing-complete.

Consider a classic computing challenge, such as identifying the majority class in a sequence of binary digits (0s and 1s). A von Neumann style computer can efficiently address this through a program like:

def get_majority(input):

counter_0, counter_1 = 0, 0

for i in input:

if i == 0:

counter_0 += 1

else:

counter_1 += 1

return int(counter_1 > counter_0)

This capability to devise solutions for numerous problems signifies the immense power of Turing-complete systems. However, an alternative perspective on computing draws inspiration from natural phenomena, leading us into the intriguing realm of cellular automata.

Section 1.1: Cellular Automata - Complexity Arising from Simplicity

Cellular automata can be visualized as grids composed of 'cells' that exist in two states, such as black and white. We can define rules governing the interactions of these cells, for example:

One notable example is 'Rule 30,' explored extensively by computer scientist Stephen Wolfram in the 1980s. In this rule, a black cell flanked by two black cells turns white, while a white cell surrounded by white cells remains unchanged. Starting with a single black cell, the application of Rule 30 generates a complex structure:

The resulting pattern reveals intricate triangular formations and seemingly random placements, demonstrating how simple deterministic rules can yield complex outcomes.

Section 1.2: Cellular Automata as Computational Systems

In 1996, researcher Melanie Mitchell and her team created a cellular automaton capable of solving the majority class problem mentioned earlier. Given a grid of black and white cells, the automaton determines which color predominates and subsequently updates all cells to reflect that majority. The initial chaotic arrangement leads to a final state where all cells are black:

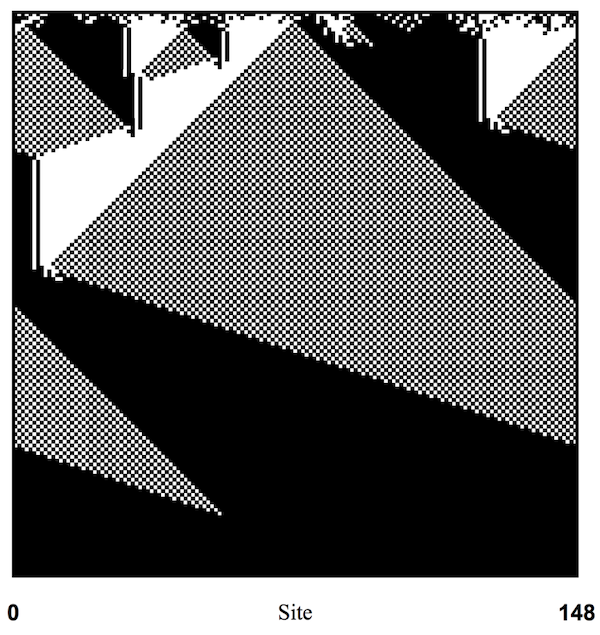
This demonstrates that cellular automata can function similarly to computers, despite lacking traditional components such as a central processing unit or memory. Instead, each cell serves as both a processing unit and a carrier of information.

However, it is crucial to note that the design of such systems often requires significant effort to tackle relatively simple problems under specific conditions. While some cellular automata have been shown to be Turing-complete—like the Game of Life and Rule 110—they remain impractical for solving complex real-world issues.

Chapter 2: Nature as a Computation Engine

The first video illustrates how natural computing principles can be observed in various phenomena.

The second video explores computer simulations that mimic natural processes, revealing the computational aspects of nature.

Cellular automata can also be observed in nature, exemplified by ant colonies. Each ant adheres to simple rules, yet collectively they exhibit sophisticated behaviors. For instance, when foraging for food, ants randomly explore their environment. If successful, they leave pheromone trails for others to follow, creating a self-reinforcing loop that optimizes the foraging process.

This decentralized computation allows the colony to effectively 'calculate' the best routes for maximizing food collection without the need for a centralized control system. The principles derived from ant behavior have even inspired algorithms for solving complex routing problems in human contexts.

Many natural phenomena, from immune responses to neuronal activity, can be framed as cellular automata. In each case, simple local rules govern the behavior of individual elements, leading to intricate and complex structures.

Ultimately, cellular automata serve as nature's solution to the intricate computational challenges inherent in survival.

If you found this exploration intriguing, consider delving into these related topics:

• The limits of knowledge: Gödel, Turing, and the science of what we can and cannot know
• The origin of intelligent behavior: Why true AI requires more than pattern recognition