Exploring Number Theory Through Modular Arithmetic Challenges
Written on
Chapter 1: Understanding Fermat’s Little Theorem
Fermat's Little Theorem provides a significant insight into number theory. Specifically, it asserts that if ( p ) is a prime number and ( a ) is an integer that is coprime to ( p ), then:

In applying this theorem to a number theory puzzle, we observe that since 7 is a prime number, the integers 2, 3, 4, 5, and 6 are all coprime to 7. This allows us to utilize the theorem to derive further results.
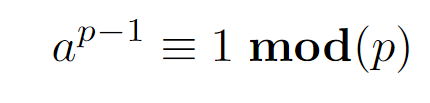
Let’s consider ( p = 7 ). Consequently, ( p - 1 = 6 ). By utilizing modular arithmetic properties, we can derive the following conclusions.
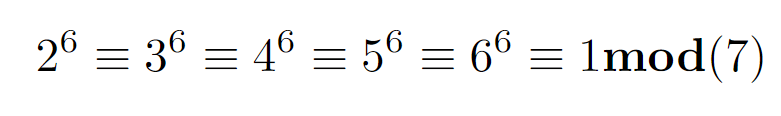
Focusing on the term ( 2^? ), we can again apply the result from Fermat’s Little Theorem to simplify our computations.
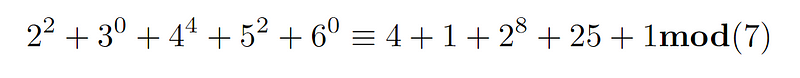
Ultimately, we find that the remainder of our summation equals 0 when divided by 7, indicating that it is indeed divisible by 7. Thus, we have reached our conclusion—Q.E.D.
Isn’t that fascinating? How did you approach this problem? Feel free to share your thoughts in the comments; I’m eager to hear your insights!
This engaging video titled "Number Theory Puzzle | A Puzzle of Ages" delves deeper into the concepts of number theory and challenges viewers with intriguing puzzles.
Math Puzzles on Medium
Explore a variety of math puzzles ranging from algebra to number theory, perfect for sharpening your problem-solving skills.
In this entertaining video, "A fun number theory puzzle by Ramanujan," the renowned mathematician’s insights into number theory are showcased through engaging challenges.
Chapter 2: Conclusion
Thank you for reading! If you found this article insightful, please consider showing your appreciation by clapping for it.

Your support means the world to me! If you appreciate the effort I put into creating these articles, consider buying me a coffee. It’s a wonderful way to contribute to my writing journey and personal growth.
Love, Bella 😊