Daily Computer Algebra Challenge

Today's focus is on demonstrating the solution to a specific integral problem.

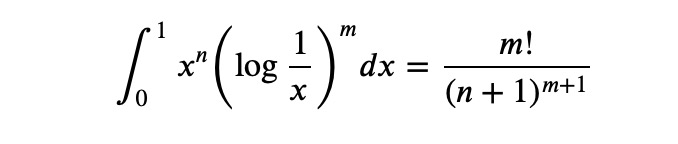
Solution Utilizing SymPy

To approach the solution with SymPy, we need to integrate a combination of assumptions, variable changes, and term rewrites. Initially, we define the necessary variables:

It is crucial to clearly identify certain variables, such as designating one as a real number and others as positive integers. Stating assumptions about these variables is essential, particularly when performing integration. Without these assumptions, SymPy may struggle with specific operations that are only applicable under certain conditions. The integral we seek to solve is:

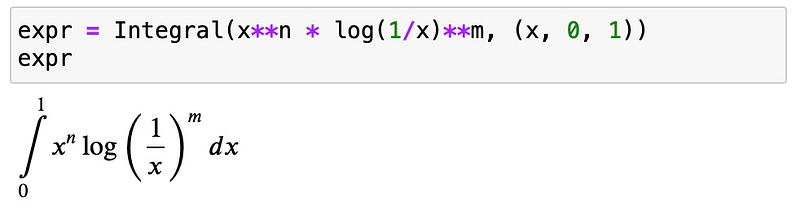
Attempting to execute expr.doit() will lead to prolonged calculations before SymPy ultimately fails. However, we can assist the process by changing the variables of integration:

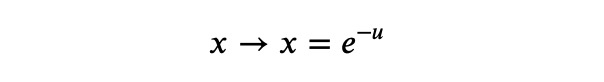
This transformation is straightforward using SymPy's transform function:

The expression now resembles a Gamma function, and with this reformulation, SymPy should be capable of resolving the integral:

We're nearing the conclusion of our solution. The final step is to express the Gamma function in terms of factorials. Since we have established that the variable is an integer, SymPy can effectively perform this transformation:

And there we have it—the integral is successfully solved!