Chapter 1: Understanding Complex Integrals

When faced with integrals that appear perplexing, it's essential to ponder: "Is this integral truly as complicated as it seems?" Following that, consider whether there's a smart way to manipulate the integrand to simplify the problem. In this instance, we can observe that a logarithmic function is present, which brings to mind the substitution method. But which substitution should we apply?

To begin, let's examine the differentiation of the logarithmic function. The derivative of ln(x) is expressed in standard formulas:

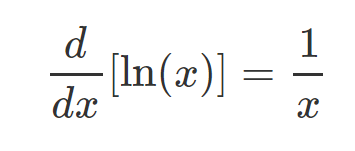
Further, we can expand this concept by recognizing that for any function ln(f(x)), the derivative can be represented as:

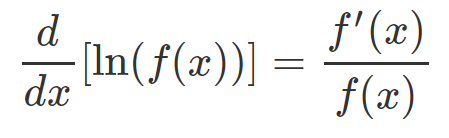
If we let f(x) = x^n, where n is greater than zero, we arrive at:

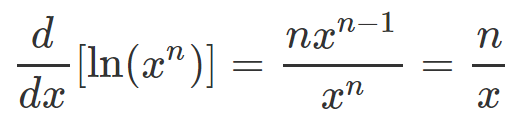
This conclusion aligns with the properties of logarithms, specifically that ln(x^n) = n * ln(x). Examining our integrand reveals a resemblance to this logarithmic function. By rewriting it as:

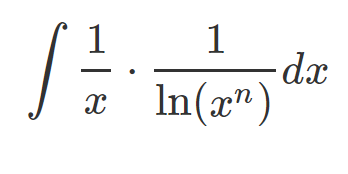
we can identify that the first part of this expression is, in fact, the derivative of ln(x^n) divided by n. Thus, we can express it more adeptly as:

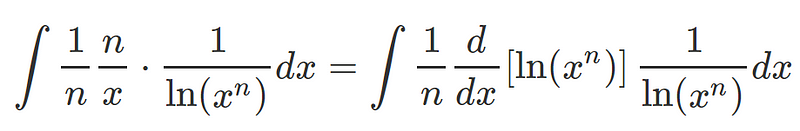
However, this approach might be overcomplicating our task. Our primary goal is to utilize a substitution. Let's define a new variable:

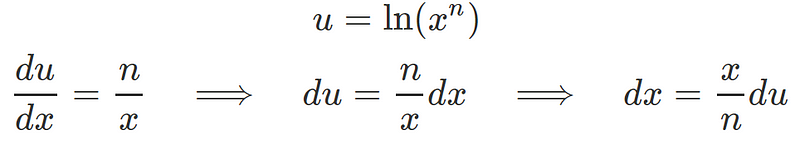
Next, we can insert these expressions into our integrand:

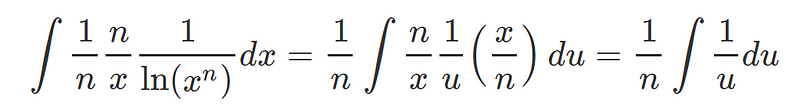
The resulting integral with respect to u is significantly more straightforward. According to standard results, we know that:

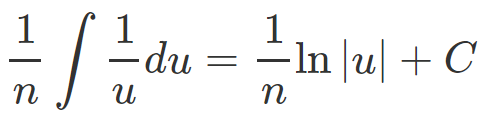
At this point, all that remains is to substitute back u = ln(x^n) into our expression:

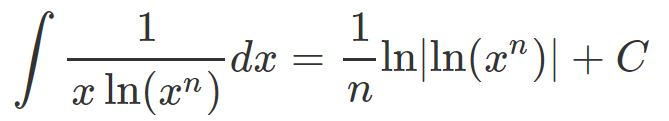
This gives us our ultimate result.

Chapter 2: Insightful Video Resources

Explore integrals that may seem challenging but can be simplified with the right techniques in this insightful video.

Learn about an easy problem contrasted with a seemingly difficult one in this engaging video.