Understanding Paint Coverage on a Rubik's Cube: An Analysis
Written on
Chapter 1: Introduction to Paint Coverage
How many sides of an 8x8x8 cube are coated in paint? This question might seem straightforward, especially if we were discussing a smaller 3x3x3 cube. It's exciting to see the rapid growth of our community, and I encourage you to share our engaging math puzzles with friends and family!
Take a moment to pause and grab your pen and paper. When you're ready, we’ll dive into the solution!
Let’s start by determining how many smaller cubes make up an 8x8x8 cube. As expected, the total number of smaller cubes is calculated as 8 × 8 × 8 = 512.
Now, we’ll analyze the cubes based on how many sides are painted: 3 sides, 2 sides, 1 side, and 0 sides.
Section 1.1: Cubes Painted on Three Sides
There are 8 corner cubes, each painted on three sides.

Section 1.2: Cubes Painted on Two Sides
Next, we need to consider the cubes located along the edges.
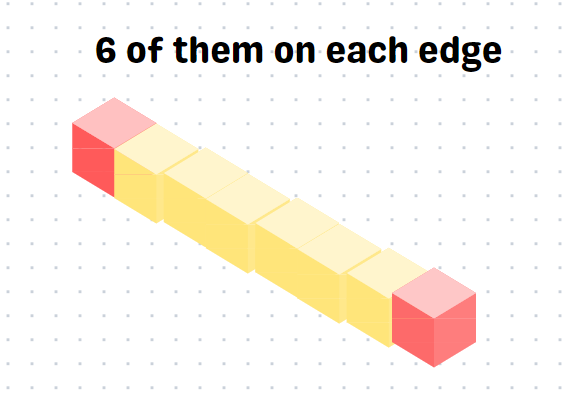
The red cubes signify the corners, while the yellow ones represent the edge cubes, which are painted on two sides. With 12 edges, there are 72 cubes painted on two sides.
Section 1.3: Cubes Painted on One Side
For cubes painted on just one side, we have:

Each face of the cube contains 6 × 6 = 36 cubes, and since there are 6 faces, the total painted on one side amounts to 36 × 6 = 216.
Section 1.4: Cubes with No Paint
Finally, the cubes that do not have any paint are those completely enclosed by the outer layer of the 8x8x8 cube.
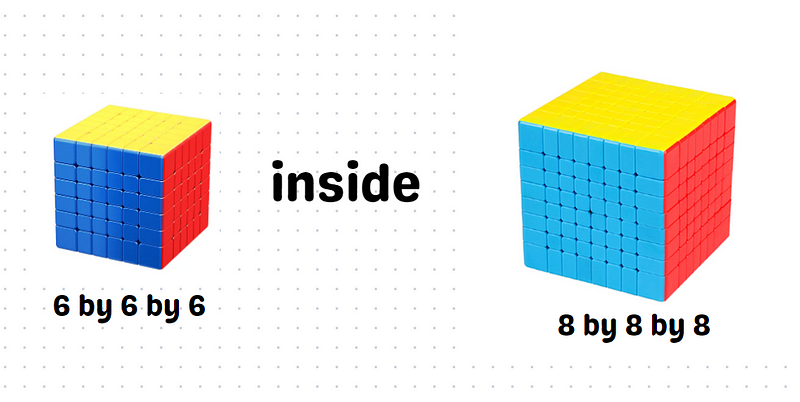
These cubes form a 6x6x6 configuration, leading to 6 × 6 × 6 = 216 cubes without any paint.
We can verify that the total number of cubes painted on 3, 2, 1, and 0 sides adds up to the overall total:
8 + 72 + 216 + 216 = 512.
Bonus Challenge: Exploring the 7x7x7 Cube
What would happen with a 7x7x7 cube? Is there a formula that can be generalized for an n x n x n cube? How fascinating!
I'd love to hear your thoughts on this challenge, so please comment below!
Chapter 2: Additional Resources
For more engaging content, check out the following videos:
In this video, titled "How to Paint 2 Sides of a Door & Frame with 2 Different Colours," you’ll learn about painting techniques that can be applied to various projects.
The second video, "18.2.2 A 10x10x10 cube is dipped in paint. How many small cubes have paint? (3+ Solutions)," explores the mathematics of paint coverage on cubes.
Thank you for reading! If you found this analysis insightful, please show your support by sharing it with others.