Points, Lines, and Conic Sections: A Sequel to College Algebra

This textbook provides a comprehensive exploration of conic sections, similar to how linear algebra is approached.

The five-star rating reflects the book's substantial value.

Chapter 2: The Theorem of Hyperbolas

In this section, we will examine a theorem concerning the interaction between a line with slope m and the focus of a right-left hyperbola, with a distance d separating the intersection points.

I have dedicated many years to uncovering the connections between m, a, b, and d. My journey took a decade to bring this work to fruition, driven solely by a thirst for knowledge regarding conic sections. While my research may not reach the complexity of Andrew Wiles’s proof of Fermat’s Last Theorem—where only a fraction of the mathematical community could grasp its depth—I believe my contributions are accessible to a broader audience.

In the diagram below, the key relationship is depicted:

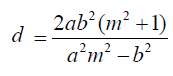
To begin our exploration, let’s solve for a², b², and m. You’ll notice the resemblance to the equations related to ellipses from my previous writings. This is intentional, and if you've grasped those concepts, you’ll find this task straightforward. The equations we derive will be:

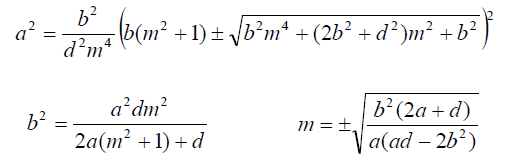
If you’ve successfully completed this, congratulations! You're now ready to tackle one of the exercises from my book.

After inputting the system into Wolfram Alpha, I obtained the following results.

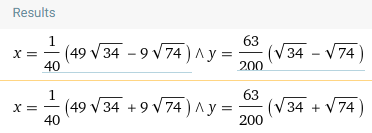
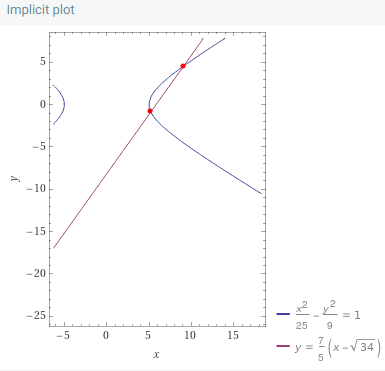
These outputs represent the (x, y) coordinates of the intersection points between the line and the hyperbola. Use the distance formula to calculate the distance, and then apply the new formula I introduced. You should arrive at the same result. This exercise will sharpen your algebraic and arithmetic skills. Here’s the graph generated by Wolfram Alpha:

Thanks for taking the time to read my insights.