Exploring Energy Dynamics in Electromagnetically Charged Black Holes
Written on
Chapter 1: Understanding Energy and Momentum in Black Holes
Greetings, fellow enthusiasts! Currently, I am delving into a fascinating paper by R. D. Blandford and R. L. Znajek titled "Electromagnetic Extraction of Energy from Kerr Black Holes." This study investigates how electromagnetic fields facilitate the transfer of energy in and out of black holes.
Flux Dynamics Around Black Holes
In the framework of general relativity, energy and momentum can be encapsulated within a single entity known as the energy-momentum tensor, which can be organized into a matrix format. For a system with five coordinates, the resulting matrix would be 5 by 5, with each row corresponding to a particular coordinate component. This tensor is subject to conservation laws, which allows us to establish a flux term. The term "flux" serves as a broad descriptor for the directional component of the tensor.
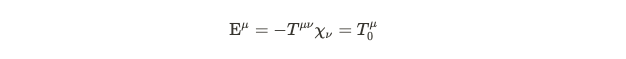
The above expression represents the electromagnetic energy flux. Additionally, we can consider angular momentum flux, focusing on the electromagnetic tensor component aligned with the axial direction. For the electromagnetic energy flux, our focus narrows to two specific directions: the radial direction (inward or outward from the center) and the theta coordinate, which aligns with lines of longitude. These two directions are recognized as the poloidal components, defined explicitly in the equations below.
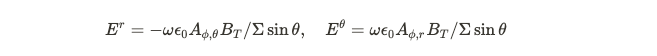
Here, Omega signifies the "angular velocity" of the magnetic field, while the symbol sigma represents a characteristic length scale dependent on the black hole's angular momentum.
Surfaces of Interest
By maintaining certain components of the electromagnetic tensor constant, we can delineate specific surfaces. The poloidal surface arises when the phi coordinate remains constant. This coordinate, which encircles the horizontal plane, produces a surface indicated by the red arrow in the illustration below.
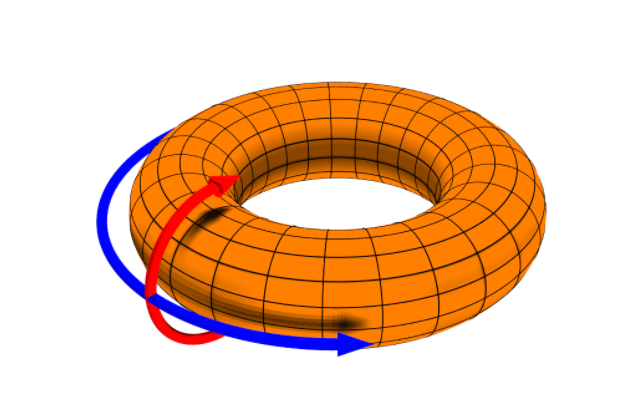
As physicists, we are particularly interested in quantities that remain unchanged on designated surfaces. According to reference [1], there exists another conserved function, denoted by the Greek letter mu, which indicates the rate of change in the vector potential as we traverse the circle along the phi axis.
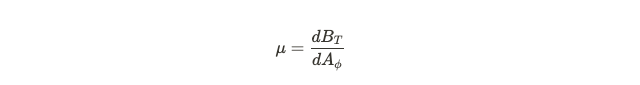
To determine the current emanating from a specific slice, we can express it with a particular equation. To ascertain the total current expelled from the black hole, we would integrate across the entire coordinate set.
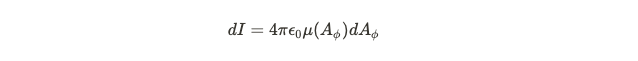
Observational Insights
What might an observer near the horizon perceive? A rotating observer would detect energy flux entering the black hole while angular momentum exits. The intriguing question arises: how rapidly is energy extracted from the black hole? Reference [1] demonstrates that black holes lose energy electromagnetically at the following rate:
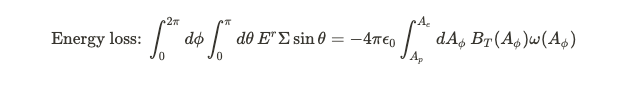
In this equation, omega represents the electromagnetic angular velocity. This interpretation seems valid since energy can be expressed as the product of omega and angular momentum, giving it the correct units. To derive the above equation, we integrate the flux over a spherical surface, keeping the radius constant while varying the phi and theta components, as depicted in the expression on the left. Integrating the theta coordinate from zero to pi corresponds to integrating the field from A_e to A_p.
Changing the coordinates leads us to the right-hand side expression (the proof of which I am still working to clarify). The metric's determinant determines the necessary scaling for the integrand. The metric g can be formulated as a matrix based on our selected coordinate system, with the determinant represented as follows:
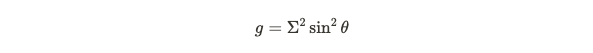
Moreover, there is a corresponding angular momentum loss from the black hole, as illustrated in the subsequent expression:
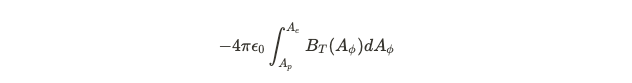
References
[1] R. D. Blandford, R. L. Znajek, Electromagnetic extraction of energy from Kerr black holes, Monthly Notices of the Royal Astronomical Society, Volume 179, Issue 3, July 1977, Pages 433–456.
Chapter 2: Thermodynamics of Supersymmetric Black Holes
In this chapter, we explore the thermodynamic properties of supersymmetric black holes, focusing on how these properties relate to energy extraction processes.
This video delves into the thermodynamic aspects of supersymmetric black holes, illustrating their unique characteristics and energy dynamics.
Chapter 3: Semiclassical Energy Fluxes in Rotating Black Holes
We will also examine semiclassical energy fluxes occurring at the inner horizon of rotating black holes, highlighting their implications for energy extraction.
This video presents an analysis of semiclassical energy fluxes at the inner horizon of rotating black holes, shedding light on the intricate processes at play.